märgid kohalik tõus ja funktsiooni vähenemine.

Funktsiooni uurimise üks peamisi ülesandeid on selle suurenemise ja kahanemise intervallide leidmine. Sellist uuringut on tuletise abil lihtne läbi viia. Sõnastame vastavad väited.

Piisav kriteerium funktsiooni suurendamiseks. Kui f'(x) > 0 intervalli I igas punktis, siis funktsioon f suureneb I võrra.

Funktsiooni vähenemise piisav kriteerium. Kui f'(x)< 0 в каждой точке интервала I, то функция f убывает на I.

Nende tunnuste tõendamine toimub Lagrange'i valemi alusel (vt punkt 19). Võtke suvalised kaks arvu x 1 ja x2 intervallist. Las x 1 seal on arv с∈(х 1, x 2), nii et

(1)

Arv c kuulub intervalli I, kuna punktid x 1 ja x2 kuuluvad I-sse. Kui f"(x)>0 x∈I korral, siis f'(с)>0 ja seega F(x) 1 )) — see tuleneb valemist (1), kuna x 2-x1 >0. See tõestab, et funktsioon f suureneb I võrra. Kui f’ (x)<0 для х∈I то f"(с)<0, и потому f(x 1 )>f (x 2 ) tuleneb valemist (1), kuna x 2-x1 >0. Tõestame, et funktsioon f väheneb I võrra.

Märkide visuaalne tähendus ilmneb füüsilisest arutluskäigust (kinnisuse huvides võtke arvesse suurenemise märki).

Olgu ajahetkel t piki y-telge liikuval punktil y-ordinaat y = f(t). Siis on selle punkti kiirus ajahetkel t võrdne f "(t) (vt joonis fig. Vahetu kiirus ). Kui f’ (t)>0 igal ajahetkel intervallist t, siis punkt liigub y-telje positiivses suunas, st kui t 1 ). See tähendab, et funktsioon f kasvab intervallil I.

Märkus 1.

Kui funktsioon f on pidev suurenemise (vähenemise) intervalli mis tahes otsas, siis on see punkt lisatud sellele intervallile.

Märkus 2.

Võrratuste f "(x)>0 ja f" (x) lahendamiseks<0 удобно пользоваться обобщением метода интервалов (теоремой Дарбу) : точки, в которых производная равна 0 или не существует, разбивают область определения функции f на промежутки, в каждом из которых f" сохраняет постоянный знак. (Этот факт доказывается в курсах математического анализа.) Знак можно определить, вычислив значение f" в какой-нибудь точке промежутка.

Vajalik ja piisavad tingimused funktsiooni ekstreemumi olemasolu punktis.

Ekstreemumi vajalik tingimus

Funktsioonil g(x) on punktis ekstreemum (maksimaalne või miinimum), kui funktsioon on määratletud punkti kahepoolses naabruses ja mõne ala kõigi punktide x jaoks: võrratus vastavalt

(maksimumi korral) või (miinimum puhul).

Funktsiooni ekstreemumi saab leida tingimusest: kui tuletis on olemas, s.o. võrdsustage funktsiooni esimene tuletis nulliga.

Piisav äärmuslik seisund

1) Esimene piisav tingimus:

a) f(x) on pidev funktsioon ja on defineeritud mõne punkti naabruses nii, et esimene tuletis antud punktis on võrdne nulliga või seda ei eksisteeri.

b) f(x)-l on funktsiooni spetsifikatsiooni ja pidevuse läheduses lõplik tuletis

c) tuletis säilitab teatud märgi punktist paremal ja samast punktist vasakul, siis saab punkti iseloomustada järgmiselt

See tingimus ei ole eriti mugav, kuna peate kontrollima palju tingimusi ja jätma tabeli meelde, kuid kui kõrgemat järku tuletistest pole midagi öeldud, on see ainus viis funktsiooni ekstreemumi leidmiseks.

2) Teine piisav tingimus

Kui funktsioonil g(x) on teine ​​tuletis ja mingil hetkel on esimene tuletis võrdne nulliga ja teine ​​tuletis on nullist erinev. Siis punkt funktsiooni äärmus g(x), ja kui , siis punkt on maksimum; kui , siis punkt on miinimum.

Funktsiooni olemuse kindlakstegemiseks ja selle käitumisest rääkimiseks on vaja leida suurenemise ja kahanemise intervallid. Seda protsessi nimetatakse funktsioonide uurimiseks ja joonistamiseks. Ekstreemumipunkti kasutatakse funktsiooni suurima ja väikseima väärtuse leidmisel, kuna need suurendavad või vähendavad funktsiooni intervallist.

See artikkel paljastab definitsioonid, sõnastame intervallile piisava suurenemise ja vähenemise märgi ning ekstreemumi olemasolu tingimuse. See kehtib näidete ja probleemide lahendamise kohta. Funktsioonide eristamise osa tuleks korrata, sest lahendamisel tuleb kasutada tuletise leidmist.

Yandex.RTB R-A-339285-1 1. definitsioon

Funktsioon y = f (x) suureneb intervallil x, kui mis tahes x 1 ∈ X ja x 2 ∈ X , x 2 > x 1 korral on ebavõrdsus f (x 2) > f (x 1) teostatav. Teisisõnu, argumendi suurem väärtus vastab funktsiooni suuremale väärtusele.

Definitsioon 2

Funktsioon y = f (x) loetakse kahanevaks intervallil x, kui mistahes x 1 ∈ X, x 2 ∈ X, x 2 > x 1 korral võetakse arvesse võrdsust f (x 2) > f (x 1) teostatav. Teisisõnu, suurem funktsiooni väärtus vastab väiksemale argumendi väärtusele. Mõelge allolevale joonisele.

Kommentaar: Kui funktsioon on tõusva ja kahaneva intervalli otstes kindel ja pidev, st (a; b) kus x = a, x = b, on punktid kaasatud kasvavasse ja kahanevasse intervalli. See ei ole definitsiooniga vastuolus, mis tähendab, et see toimub intervallil x.

Tüüpi y = sin x elementaarfunktsioonide põhiomadused on argumentide reaalväärtuste täpsus ja järjepidevus. Siit saame, et siinuse suurenemine toimub intervallil - π 2; π 2, siis on segmendi suurenemine kujul - π 2; π 2 .

Punkti x 0 nimetatakse maksimaalne punkt funktsiooni y = f (x) korral, kui kõigi x väärtuste korral on ebavõrdsus f (x 0) ≥ f (x) tõene. Funktsiooni maksimum on funktsiooni väärtus punktis ja seda tähistatakse y m a x .

Punkti x 0 nimetatakse funktsiooni y \u003d f (x) miinimumpunktiks, kui kõigi x väärtuste korral on ebavõrdsus f (x 0) ≤ f (x) tõene. Funktsiooni miinimum on funktsiooni väärtus punktis ja selle tähistus on kujul y m i n .

Arvesse võetakse punkti x 0 ümbrust äärmuslikud punktid, ja äärmuspunktidele vastava funktsiooni väärtus. Mõelge allolevale joonisele.

Funktsiooni suurima ja väikseima väärtusega funktsiooni äärmus. Mõelge allolevale joonisele.

Esimene joonis ütleb, et on vaja leida funktsiooni suurim väärtus segmendist [ a ; b] . See leitakse maksimaalsete punktide abil ja võrdub funktsiooni maksimaalse väärtusega ning teine ​​arv on rohkem nagu maksimumpunkti leidmine x = b.

Piisavad tingimused funktsioonide suurendamiseks ja vähendamiseks

Funktsiooni maksimumide ja miinimumide leidmiseks on vaja rakendada ekstreemumi märke juhul, kui funktsioon neid tingimusi täidab. Esimene funktsioon on kõige sagedamini kasutatav.

Ekstreemumi esimene piisav tingimus

Olgu antud funktsioon y = f (x), mis on diferentseeruv punkti x 0 naabruses ε ja millel on pidevus antud punktis x 0 . Seetõttu saame selle kätte

• kui f "(x) > 0, kui x ∈ (x 0 - ε; x 0) ja f" (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• kui f"(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 x ∈ (x 0 ; x 0 + ε) korral, siis x 0 on miinimumpunkt.

Teisisõnu saame nende märgi seadmise tingimused:

• kui funktsioon on pidev punktis x 0, siis on tal muutuva märgiga tuletis, st + -st -, mis tähendab, et punkti nimetatakse maksimumiks;
• kui funktsioon on pidev punktis x 0, siis on tal tuletis muutuva märgiga -st +-ni, mis tähendab, et punkti nimetatakse miinimumiks.

Funktsiooni maksimum- ja miinimumpunktide õigeks määramiseks peate järgima nende leidmise algoritmi:

• leida määratluspiirkond;
• leida sellel alal funktsiooni tuletis;
• tuvastada nullid ja punktid, kus funktsiooni ei eksisteeri;
• tuletise märgi määramine intervallidel;
• valige punktid, kus funktsioon muudab märki.

Vaatleme algoritmi mitme funktsiooni äärmuse leidmise näite lahendamise näitel.

Näide 1

Leia antud funktsiooni y = 2 (x + 1) 2 x - 2 maksimum- ja miinimumpunktid.

Otsus

Selle funktsiooni domeeniks on kõik reaalarvud, välja arvatud x = 2. Esiteks leiame funktsiooni tuletise ja saame:

y "= 2 x + 1 2 x - 2" = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2)" (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2) ) - (x + 2) 2 (x) - 2) 2 = = 2 (x + 1) (x - 5) (x - 2) 2

Siit näeme, et funktsiooni nullid on x \u003d - 1, x \u003d 5, x \u003d 2, see tähendab, et iga sulg tuleb võrdsustada nulliga. Märgi numbrireale ja saad:

Nüüd määrame iga intervalli tuletise märgid. Vaja on valida intervalli kuuluv punkt, asendada see avaldisega. Näiteks punktid x = - 2, x = 0, x = 3, x = 6.

Me saame sellest aru

y "(- 2) \u003d 2 (x + 1) (x - 5) (x - 2) 2 x \u003d - 2 \u003d 2 (- 2 + 1) (- 2 - 5) (- 2 - 2) ) 2 \u003d 2 7 16 \u003d 7 8 > 0, seega on intervallil - ∞; - 1 positiivne tuletis. Samamoodi saame, et

y "(0) = 2 (0 + 1) 0 - 5 0 - 2 2 = 2 - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Kuna teine ​​intervall osutus nullist väiksemaks, tähendab see, et segmendi tuletis on negatiivne. Kolmas miinusega, neljas plussiga. Järjepidevuse määramiseks on vaja pöörata tähelepanu tuletise märgile, kui see muutub, siis on tegemist ekstreemumipunktiga.

Saame, et punktis x = - 1 on funktsioon pidev, mis tähendab, et tuletis muudab märgi + asemel -. Esimese märgi järgi on meil, et x = - 1 on maksimumpunkt, mis tähendab, et saame

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

Punkt x = 5 näitab, et funktsioon on pidev ja tuletis muudab märgi - asemel +. Seega on x=-1 miinimumpunkt ja selle leidmisel on vorm

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

Graafiline pilt

Vastus: y m a x = y (- 1) = 0, y m i n = y (5) = 24 .

Tähelepanu tasub pöörata asjaolule, et ekstreemumi esimese piisava märgi kasutamine ei eelda, et funktsioon oleks diferentseeruv punktist x 0 ja see lihtsustab arvutamist.

Näide 2

Leia funktsiooni y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 maksimum- ja miinimumpunktid.

Otsus.

Funktsiooni domeeniks on kõik reaalarvud. Selle saab kirjutada võrrandisüsteemina järgmisel kujul:

1 6 x 3 - 2 x 2 - 22 3 x - 8, x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Seejärel peate leidma tuletise:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 a" = - 1 2 x 2 - 4 x - 22 3, x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

Punktil x = 0 ei ole tuletist, kuna ühepoolsete piiride väärtused on erinevad. Saame selle:

piir y "x → 0 - 0 = piir y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 piir y "x → 0 + 0 = piir y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

Sellest järeldub, et funktsioon on pidev punktis x = 0, siis arvutame

piir x → 0 - 0 = piir x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 (0 - 0) 3 - 2 (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = piir x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 ( 0 + 0) 2 + 22 3 (0 + 0) - 8 = - 8 a (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

Argumendi väärtuse leidmiseks tuleb teha arvutused, kui tuletis muutub nulliks:

1 2 x 2 - 4 x - 22 3, x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3, x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

Kõik saadud punktid tuleb joonele märkida, et määrata iga intervalli märk. Seetõttu on vaja tuletis arvutada iga intervalli suvalistes punktides. Näiteks võime võtta punkte väärtustega x = - 6 , x = - 4 , x = - 1 , x = 1 , x = 4 , x = 6 . Me saame sellest aru

y " (- 6) \u003d - 1 2 x 2 - 4 x - 22 3 x \u003d - 6 \u003d - 1 2 - 6 2 - 4 (- 6) - 22 3 \u003d - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 a "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 a "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Sirgjoonel oleval kujutisel on vorm

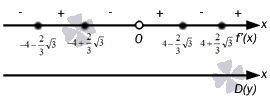
Niisiis, jõuame selleni, et on vaja kasutada ekstreemumi esimest märki. Me arvutame ja saame selle

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , siis siit alates on maksimumpunktide väärtused x = - 4 + 2 3 3 , x = 4 - 2 3 3

Liigume edasi miinimumide arvutamise juurde:

a m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 a m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 a m i n = a 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Arvutame välja funktsiooni maksimumid. Me saame sellest aru

a m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 a m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Graafiline pilt

Vastus:

a m i n = y - 4 - 2 3 3 = - 8 27 3 a m i n = y (0) = - 8 a m i n = a 4 + 2 3 3 = - 8 27 3 a m a x = a - 4 + 2 3 3 = 3 8 m 2 = y 4 - 2 3 3 = 8 27 3

Kui funktsioon f "(x 0) = 0 on antud, siis selle f "" (x 0) > 0 abil saame, et x 0 on miinimumpunkt, kui f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Näide 3

Leia funktsiooni y = 8 x x + 1 maksimumid ja miinimumid.

Otsus

Esiteks leiame määratluspiirkonna. Me saame sellest aru

D (y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

On vaja eristada funktsiooni, mille järel saame

y "= 8 x x + 1" = 8 x " (x + 1) - x (x + 1)" (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

Kui x = 1, võrdub tuletis nulliga, mis tähendab, et punkt on võimalik ekstreemum. Selguse huvides on vaja leida teine ​​tuletis ja arvutada väärtus x \u003d 1 juures. Saame:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x "(x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2" x + (x + 1) 2 x "(x + 1) 4 x == 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1)" x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 - 4 8 = - 1< 0

Seega, kasutades ekstreemumi jaoks piisavat tingimust 2, saame, et x = 1 on maksimumpunkt. Vastasel juhul on kirje y m a x = y (1) = 8 1 1 + 1 = 4 .

Graafiline pilt

Vastus: y m a x = y (1) = 4 ..

Funktsiooni y = f (x) tuletis on kuni n-ndat järku antud punkti x 0 naabruses ε ja selle tuletis kuni n + 1. järku punktis x 0 . Siis f "(x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0.

Sellest järeldub, et kui n on paarisarv, siis x 0 loetakse käändepunktiks, kui n on paaritu arv, siis x 0 on äärmuspunkt ja f (n + 1) (x 0) > 0, siis x 0 on miinimumpunkt, f(n+1)(x0)< 0 , тогда x 0 является точкой максимума.

Näide 4

Leia funktsiooni y y = 1 16 (x + 1) 3 (x - 3) 4 maksimum- ja miinimumpunktid.

Otsus

Algne funktsioon on terve ratsionaalne funktsioon, seega järeldub, et määratluspiirkond on kõik reaalarvud. Funktsioon tuleb eristada. Me saame sellest aru

y "= 1 16 x + 1 3" (x - 3) 4 + (x + 1) 3 x - 3 4 " == 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

See tuletis läheb nulli, kui x 1 = - 1, x 2 = 5 7, x 3 = 3. See tähendab, et punktid võivad olla võimaliku ekstreemumi punktid. Vaja on rakendada kolmandat piisavat äärmuse tingimust. Teise tuletise leidmine võimaldab täpselt määrata funktsiooni maksimumi ja miinimumi olemasolu. Teine tuletis arvutatakse selle võimaliku ekstreemumi punktides. Me saame sellest aru

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

See tähendab, et x 2 \u003d 5 7 on maksimumpunkt. Rakendades 3 piisavat kriteeriumi, saame, et n = 1 ja f (n + 1) korral 5 7< 0 .

On vaja kindlaks määrata punktide olemus x 1 = - 1, x 3 = 3. Selleks peate leidma kolmanda tuletise, arvutama nende punktide väärtused. Me saame sellest aru

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " == 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Seega on x 1 = - 1 funktsiooni käändepunkt, kuna n = 2 ja f (n + 1) (- 1) ≠ 0 korral. On vaja uurida punkti x 3 = 3 . Selleks leiame 4. tuletise ja teostame siinkohal arvutused:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " == 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

Ülaltoodust järeldame, et x 3 \u003d 3 on funktsiooni miinimumpunkt.

Graafiline pilt

Vastus: x 2 \u003d 5 7 on antud funktsiooni maksimumpunkt, x 3 \u003d 3 - antud funktsiooni minimaalne punkt.

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Olgu f lõigul pidev ja diferentseeruv selle lõigu sisemistes punktides. Seejärel on sellel lõigul sisepunkt, nii et funktsiooni graafiku puutuja, mis on tõmmatud punktis abstsissiga c, on paralleelne kõõluga AB, kus A(a; f(x)) ja B( b; f(x)). Või: sujuval kaarel AB on alati punkt c, mille puutuja on paralleelne kaare otste ühendava kõõluga.

Olgu f lõigul pidev ja diferentseeruv selle lõigu sisemistes punktides. Siis on sellest segmendist selline sisepunkt, et

Järeldus 1: kui funktsioon f on lõigul pidev ja selle tuletis on selle lõigu sees võrdne nulliga, siis on funktsioon f segmendil konstantne.

Järeldus 2: kui funktsioonid f ja g on lõigul pidevad ja neil on selle lõigu sees samad tuletised, siis erinevad need konstantse liikme poolest.

2. Piisav märk funktsiooni suurenemisest:

Kui f[/](x)>0 intervalli I igas punktis, siis funktsioon f suureneb intervallil I.

3. Piisav kriteerium funktsiooni vähendamiseks:

Kui f[/](x)

Tõestame neid märke Lagrange'i valemiga:

Võtke suvalised kaks numbrit ja intervallist. Las olla. Lagrange'i valemi järgi on selline arv, et.

Arv c kuulub intervalli I, kuna punktid ja kuuluvad sellesse intervalli. Kui f[/](x)>0 jaoks, siis f[/](c) >0 ja seega - see tuleneb valemist (1), kuna ->0. See tõestab, et funktsioonid f suurenevad intervallil I. Kui f[/](x) 0, siis funktsioon f väheneb intervallil I.

Näide 1. leidke suureneva ja kahaneva funktsiooni intervallid

2. Leia funktsiooni ja selle kriitiliste punktide tuletis: või

3. Märgistame reaalteljel ekstreemumite punktid ja leiame funktsiooni suurenemise ja vähenemise intervallid

Vastus: - funktsioon suureneb

Funktsioon väheneb

Näide 2. Uurige funktsiooni suurendamist (langetamist):

2. Leia funktsiooni tuletis- ja ekstreemumipunktid:

3. Märgime arvuteljele kriitilise punkti ja leiame funktsiooni suurenemise (vähenemise) intervallid:

Vastus: - funktsioon väheneb

Funktsioon tõuseb

II. kriitilised punktid. Funktsiooni maksimumi ja miinimumi leidmise märgid.

1. Kriitilised punktid

Definitsioon: funktsiooni kriitilised punktid on funktsiooni domeeni sisemised punktid, kus selle tuletis on võrdne nulliga või seda ei eksisteeri.

nr 1. Leia funktsiooni f kriitilised punktid: a) g(x) =

Vastus: kus; , kus b) g(x) =

2. Funktsiooni maksimumi ja miinimumi leidmise märgid.

Funktsioonide maksimumi märk:

Kui funktsioon f on pidev punktis x0 ja f[/](x)>0 intervallil (a;x0) ja f[/](x)

Või: kui punktis x0 tuletis muudab märgi plussist miinusesse, siis on x0 maksimumpunkt.

Tõestus:

Tuletis f[/](x)>0 intervallil (a; x0) ja funktsioon on pidev punktis x0, seega funktsioon f suureneb intervallil (a; x0] ja seetõttu f(x)

Intervallil [x0; c) funktsioon väheneb ja seetõttu f(x)

Funktsiooni miinimummärgid:

Kui funktsioon f on pidev punktis x0 ja f[/](x) 0 intervallil (x0;v), siis on punkt x0 funktsiooni f miinimumpunkt.

Või: kui punktis x0 tuletis muudab märgi miinusest plussiks, siis x0 on miinimumpunkt.

Tõestus:

Tuletis f[/](x) f (x0) kõigi x intervalli (a;x0) jaoks.

Intervallil [x0; c) funktsioon f suureneb ja seetõttu f(x) > f (x0) kõigi jaoks alates intervallist (a; c), st x0 on f miinimumpunkt.

III. Teine tuletis. Märgid kumerusest ja nõgususest.

Olgu punktis olemas ka teine ​​tuletis. Siis, kui, siis punkt on miinimumpunkt ja kui, siis punkt funktsiooni maksimumpunkt.

Kui, siis on kumerus suunatud allapoole. Kui, siis on kumerus suunatud ülespoole.

IV. Kaldus asümptoodid

Definitsioon: Sirge on funktsioonigraafiku kaldus asümptoot, kus ja

Kaldus asümptoodi võrrand

Vertikaalsed asümptoodid kaldu asümptoodi võrrand

V. Funktsiooniuuringute kava

1. Leidke funktsiooni domeen.

2. Uurige funktsiooni tasasuse (veidruse) jaoks.

3. Leidke graafiku lõikepunktid koordinaattelgedega ja määrake funktsiooni märgi intervallid.

4. Leia tuletis.

5. Leia funktsiooni äärmuspunktid ning funktsiooni suurenemise ja kahanemise intervallid.

6. Tee laud.

7. Leia teine ​​tuletis.

8. Leidke funktsiooni graafiku käändepunktid ja määrake selle graafiku kumeruse ja nõgususe intervallid.

9. Leia vajadusel funktsiooni graafiku asümptoodid.

10. Koostage selle funktsiooni graafiku visand.

11. Leia funktsiooni väärtuste hulk.

VI. Näited funktsiooniuuringu kohta

2). Funktsiooni paarsusest ei saa rääkida.

5) Leidke funktsiooni äärmuspunktid ning funktsiooni suurenemise ja kahanemise intervallid:

Funktsioon tõuseb

Funktsioon väheneb

6) Teeme tabeli x

7) Leia teine ​​tuletis

8) Leidke pöördepunktid: või

punnis üles

kumeraks allapoole

9) Otsida kaldus asümptoote ei eksisteeri. kaldus asümptoote pole.

10) Graafik

; x=2 – vertikaalne asümptoot

2). Funktsiooni paarsusest ei saa rääkida

3) Leia graafiku lõikepunktid OX-teljega.

Leiame graafiku lõikepunktid y-teljega.

4) Leidke funktsiooni tuletis:

5) Leidke funktsiooni äärmuspunktid ning funktsiooni kasvu- ja languspunktid:

Funktsioon tõuseb

Funktsioon väheneb

6) Teeme tabeli x

7) Leidke teine ​​tuletis:

8) Leidke pöördepunktid: pöördepunkte pole

kumeraks allapoole

punnis üles

Kaldus asümptoodi võrrand

10) Graafik

Vertikaalne asümptoot

2) funktsiooni ühtlusest ei saa rääkida

OX-teljega lõikepunkte pole.

Ei eksisteeri. Selliseid punkte pole.

4) Leidke tuletis:

Funktsioon väheneb

Funktsioon tõuseb

6) Teeme tabeli:

7) Koostame funktsiooni graafiku:

Vertikaalne asümptoot

2) - funktsiooni ühtlusest ei saa rääkida

3) Leia graafiku lõikepunktid OX-teljega.

Leiame graafiku lõikepunktid OY teljega.

4) Leidke tuletis:

5) Leia funktsiooni äärmuspunktid ning funktsiooni suurenemise ja kahanemise intervallid.

Kriitilised punktid puuduvad.

Maksimaalseid ja minimaalseid punkte pole.

6) Teeme tabeli:

↘ 7) Leidke teine ​​tuletis:

8) Leidke funktsioonigraafiku käändepunktid ja määrake kumerus- ja nõgususvahemikud:

Murdepunkte pole.

punnis üles

kumeraks allapoole

9) Leidke kaldus asümptoote:

Horisontaalne asümptoodi võrrand, kuna k = 0.

10) Koostame funktsiooni graafiku:

; - vertikaalsed asümptoodid

2) on paaritu funktsioon, kuna. Graafik on lähtekoha suhtes sümmeetriline.

3) Leia graafiku lõikepunktid OX-teljega.

Leiame graafiku lõikepunktid OY teljega.

4) Leidke tuletis:

5) Leidke suurenemise ja kahanemise funktsiooni äärmuspunktid ja intervallid:

Otsust ei ole.

Funktsioon väheneb

Funktsioon tõuseb

6) Teeme tabeli:

↘ Pole olemas.

↗ 7) Leidke kaldus asümptoote:

Kaldus asümptoote pole.

8) Leidke teine ​​tuletis:

9) Leidke pöördepunktid: või või

kumeraks allapoole

punnis üles

10) Koostame graafiku

VII. Ajaloo viide.

Lõpp oli hoopis teistsugune. elutee teine ​​matemaatilise analüüsi looja - Gottfried Wilhelm Leibniz (1646 - 1716). Aga kõigepealt asjad kõigepealt.

Tema esivanemad olid pärit Poolast ja kandsid perekonnanime Lubenitz. Pärast Leipzigisse kolimist "hakati nende perekonnanime hääldama saksapäraselt. Huvitav on märkida, et selle linna enda nimi on samuti slaavi keel, see tähendab\u003e. Leibniz sündis filosoofiaprofessori perekonda kl. Leipzigi ülikoolis kaotas ta varakult oma vanemad: 6-aastaselt jäi ta isata ja 17-aastaselt emata. Kooliajal hämmastas Leibniz oma õpetajaid oskusega koostada ladina ja kreeka keel kirg filosoofia ja matemaatika vastu. Teda eristas suur uudishimu, ta õppis paljusid aineid iseseisvalt, enne nendega kohtumist koolis. Tema mälu oli ebaühtlane: talle jäid kergesti meelde keerulised asjad ja veel hullem – lihtsad; ei osanud pikka aega arvutusi teha, kuid kaldus üldistuste ja abstraktsioonide poole. Ja selline mälestus ja mõtteviis jäi Leibnizile kogu eluks.

15-aastaselt õppis Leibniz Leipzigi ülikooli filosoofiateaduskonnas. See teaduskond valmistas ette õigusteadust ja teoloogiat. Pärast filosoofia- ja seejärel õigusteaduskonna hiilgavalt lõpetamist ei saanud 20-aastane Leibniz oma kodulinnas soovitud kohta. Konservatiivne kord ülikoolis seadis doktorikraadi omandamisele materiaalsed tõkked. Ta sõidab Nürnbergi ja kaitseb sealses ülikoolis enneolematu eduga oma õigusteaduse doktorikraadi. Märgati noore teadlase erakordset annet. Diplomaatilisse teenistusse kutsub teda Mainzi linna kuurvürst (vürst, kellel on õigus valida kuningat) ja hiljem Hannoveri hertsog.

Kui Leibniz viibis Pariisis valija äritegevuses, kohtus ta paljude kuulsate teadlastega. Arutelud erinevaid probleemeäratas temas huvi matemaatika vastu. Hiljem meenutas ta kirjas I. Bernoullile: >. Pärast ülikooli lõpetamist (1666) avaldas Leibniz filosoofilise ja matemaatilise töö, nii et omast rääkides pidas ta silmas teadmatust matemaatika viimastest saavutustest. Et tutvuda uute tulemuste ja ideedega, mis tol ajal matemaatikas tekkisid, pöördus ta abi saamiseks Huygensi poole. Ta soovitab tal mitmeid teoseid hoolikalt uurida ja Leibniz asub tööle kadestamisväärse innuga: uurib Saint-Vincenti ja Wallise, Descartes'i ja Pascali teoseid ning tegeleb oma uurimistööga.

Kuid kui ta läheb Londonisse diplomaatilise äriga ja teatab oma tulemustest inglise matemaatikutele, on ta üllatunud, kui saab teada, et paljud neist tulemustest on neile juba teada Newtoni käsikirjast, mis on talletatud Kuninglikus Ühingus. Leibniz kirjutab selle seltsi sekretäri Oldenburgi (1615 - 1677) kaudu Newtonile oma tööst. Samas kirjas palub ta Newtonil oma tulemused teatada. Vastuseks saab ta (taas Oldenburgi kaudu) kaks kirja, milles Newton selgitab seeriate abil diferentseerimise ja integreerimise toiminguid.

Leibniz ei kiirustanud oma tulemusi uues arvutuses avaldama, oodates võib-olla Newtoni väljaandeid. Kuid 1683. aastal avaldas Chirnhaus artikli algebraliste kõverate kvadratuuri kohta. Selles ei mainita Leibnizi nime, kuigi Chirnhaus võlgnes talle nende probleemide lahendamisel palju. Selleks, et peopesa selles piirkonnas püsiks, tuleb Leibniz sisse järgmine aasta prindib artikli > ja aasta hiljem - >. Esimene neist sisaldas diferentsiaalarvutuse põhitõdesid, teine ​​- integraali.

Ta pani uue teaduse aluseks diferentsiaali mõiste. Nüüd on funktsiooni y \u003d f (x) diferentsiaal df (x0) punktis x0 valemiga df (xo) \u003d f "(xo) dx, kus f" (xb) on tuletis, mis arvutatakse punktis x0 punkt xo, nende on argumendi juurdekasv. Leibniz defineerib diferentsiaali iseloomuliku kolmnurga ühe jalana, millest oli juttu eelmises peatükis (9. jagu). Joonis 46 näitab, et need määratlused on samaväärsed.

Leibniz annab reeglid summa, vahe, korrutise, jagatise, astme diferentsiaali arvutamiseks, lahendab diferentsiaalvõrrandeid. Integraali defineerib ta diferentsiaalide summana, rõhutades diferentseerimise ja integreerimise operatsioonide vastastikust pöördvõrdelisust: >. Kust järgneb integraalide omadused ja nende arvutamise meetodid. Järgmistes artiklites töötas Leibniz välja uue analüüsi. Ta tõestas, et iga integreeritav funktsioon on piiratud (integreeritavuse vajalik tingimus), töötas välja teatud tüüpi integraalide arvutamise algoritmi, eriti meetodi ratsionaalsete funktsioonide integreerimiseks. Selle meetodi väärtust ei saa ülehinnata, kuna erinevate asenduste abil taandatakse palju erinevaid integraale ratsionaalsete funktsioonide integraalideks. Vaatleme seda meetodit üksikasjalikumalt.

Suvaliste funktsioonide integreerimise probleemi graafiliseks lahendamiseks leiutas Leibniz (1693) mehaanilise seadme - integraatori. Kui liigutate selle seadme ühte tihvti mööda funktsiooni graafikut, siis teine ​​joonistab antiderivaadi graafiku.

Kasutame Leibnizi tänaseni välja töötatud algoritme ja tähistusi, aga ka enamikku tema kasutusele võetud matemaatikaterminitest: funktsioon, muutuja, konstant, koordinaadid, abstsiss, algoritm, diferentsiaal jne. Paljusid neist terminitest kasutati ka varem, kuid siiski kasutati. ei oma konkreetset tähendust, mis neile Leibnizi andis.

Järgmise sajandi alguses puhkes tuline arutelu analüüsi leiutamise prioriteedi üle. Selle põhjuseks oli Leibnizi ülevaade (1704) Newtoni loomingust, kus ta tõi välja Newtoni ja Fabry lõpmatu väikese tõlgenduse ideoloogilise ühtsuse. Taoline suure inglase võrdlus vähetuntud prantsuse matemaatiku Hon o're Fabryga (1607 - 1688) tekitas > inglise teadlaste nördimust. (Kuid Leibnizil polnud varjamisi motiive; see oli lihtsalt see, et Fabry raamat oli üks väheseid, mis aitas tal Pariisi perioodil likvideerida.) Nad nägid seda Newtoni teenete halvustamisena ja nii see algas. Selles vaidluses kaitsesid Newtoni õigusi inglise teadlased ja Leibnizi - mandri teadlased. Leibnizi toetus enamiku mandri matemaatikute poolt seletati asjaoluga, et tema tähistus osutus nii täiuslikuks ja õpetus ise nii ligipääsetavaks, et nad leidsid kohe toetajaid paljude Euroopa teadlaste seas, mis on uue teooria puhul äärmiselt haruldane. ilmub.

Ilmselt pidas tähelepanuväärne vene luuletaja Valeri Brjusov just seda vaidlust silmas, kui ta neid ridu kirjutas:

O Leibniz, oo tark, prohvetlike raamatute looja! Sa olid maailmast kõrgemal, nagu muistsed prohvetid. Sinu vanus, imestades sind, ei jõudnud ettekuulutusteni Ja segas meeletuid etteheiteid meelitustega.

Tegelikult olid mõlema poole väited alusetud. Mõlemad teadlased jõudsid iseseisvalt diferentsiaal- ja integraalarvutuse loomiseni ning nende lähenemisviisid olid täiesti erinevad. Newton kasutas võimsusridade aparaati ja Leibniz - diferentsiaali mõistet. Tuline vaidlus viis selleni, et Inglise matemaatikud eirasid kõike, mis Leibnizilt ja tema koolilt tuli, ning mandri matemaatikud brittide tööd. Kuna kontinendil tugineti Leibnizi sümboolikale, mis oli täiuslikum kui Newtoni oma, ja teadlasi ühendasid ühised avaldatud ja kõigile kättesaadavad ideed, läksid mandri matemaatikud Newtoni järgsel perioodil ingliskeelsetega võrreldes kaugele ette.

Ent Leibnizi saatuses mängis saatuslikku rolli vaen inglise ja mandri matemaatikute vahel. Hertsog, kelle jaoks ta oli raamatukoguhoidja, ajaloolane ja biograaf, olles saanud (1714) Inglise kuningaks, lahkus Londonisse. Leibniz ei saanud teda järgida, kuna tema suhted inglise matemaatikutega olid kahjustatud. Lisaks oli hertsog rahulolematu oma historiograafiga, arvates, et too ei pööranud piisavalt tähelepanu oma otsestele ametiülesannetele. Leibniz pidi jääma hertsogi raamatukogusse tööle. Äsja küpsetatud Inglise kuninga ebasoosingus viis teadlase keskkond tugevasti hõrenemiseni. Ta suri kaks aastat hiljem, tema viimasele teekonnale saatsid vaid sekretär ja matjad. Saatuse solvav ülekohus suure teadlase suhtes, kes tegi palju.

Vaatamata sellele, et Leibniz oli väga hõivatud hertsogimaja ajaloo koostamisega, millest sai Lääne-Euroopa ajalugu, ja muudest teadusest eemale viivatest ülesannetest, jättis Leibniz palju töid matemaatika, filosoofia, bioloogia, teadmiste teooria, poliitika, õiguse ja keeleteaduse kohta. Mitmekülgselt andekas teadlane andis hindamatu panuse kõigis neis valdkondades. Ideid voolas temast nagu küllusesarvest: iga kiri, iga märkus või artikkel sisaldas vaadeldavas teadusvaldkonnas midagi põhimõtteliselt uut, määrates kohati selle edasise arengu. Tema otsesel osalusel on palju ära tehtud. Berliinis organiseeris ta teadusseltsi, mis hiljem muudeti Berliini Teaduste Akadeemiaks ja sai selle esimeseks presidendiks. Ta oli esimene Pariisi Teaduste Akadeemia välisliige. Leibniz kohtus Berliinis korduvalt Peeter I-ga, kelle jaoks töötas ta välja hulga projekte Venemaa hariduse ja riigivalitsemise arendamiseks ning Peterburi Teaduste Akadeemia loomiseks.

Kuid kõige olulisem oli tema panus matemaatikasse. Sellesse sisenedes suutis ta selle täielikult muuta. Pärast tema ja tema lähimate kaastöötajate tööd ei ilmunud mitte ainult matemaatiline analüüs, vaid kogu matemaatika astus uude ajastusse.

Tundide ajal:

Õpilaste tegevused

Vahendid

2 minutit

I. Organisatsioonimoment.

Tervitan õpilasi,kontrollib tunniks valmisolekut, soovib edu.

Mõelge eesmärgi üle.

märkmikud

5 min

II. Kodutöö kontrollimine: nbh lahendada lahendamata ülesandeid, selgitada.

Näidake oma teadmisi.

tabelid

10 minutit

II. Uue teema uurimine

Kui selle funktsiooni tuletis on positiivne kõigi x väärtuste korral intervallis ( a;sisse), st. f"(x) > 0, siis funktsioon selles intervallis suureneb.
Kui selle funktsiooni tuletis on kõigi väärtuste puhul negatiivne X intervallis ( a;sisse), st. f"(x) < 0, то функция в этом интервале убывает.

Monotoonsuse intervallide leidmise järjekord:

Leidke funktsiooni ulatus.

Leia funktsiooni esimene tuletis.

Leida kriitilised punktid, uurida esimese tuletise märki intervallides, milleks leitud kriitilised punktid funktsiooni domeeni jagavad.

Leia funktsioonide monotoonsuse intervallid.

Uurime saadud intervallides tuletise märki, lahendus esitatakse tabeli kujul.

Piisavaks tingimuseks maksimumi olemasoluks on tuletise märgi muutmine kriitilise punkti läbimisel "+"-lt "-"-ks, miinimumi puhul "-"-lt "+"-ks. Kui tuletis kriitilist punkti läbides märki ei muuda, siis ekstreemumit selles punktis ei ole.

Vaatleme mõningaid näiteid suurenemise ja vähenemise funktsiooni uurimisest.

Leia funktsioonide suurenemise ja kahanemise intervallid

1) f(x) = 3–0,5x,

2) f(x) = - x2+2x-3,

3) f(x) = 4x-5,

4) f(x) = 5x 2- 3x+1.

(-∞;1)-suureneb, (1;+∞)-väheneb

(-∞;+∞)-suureneb

(-∞;0,3)-suureneb, (0,3;+∞)-väheneb

(-∞;+∞)-väheneb

Näidake oskusi.

plakatid

Valemid

Õpik

min

IV. Teadmiste kinnistamine Töö õpikuga nr 258, nr 261

3. Leida statsionaarsed punktid, st. punktid kus f"( x) = 0 või f"( x) ei eksisteeri.
(Tuletis on 0 lugeja nullidel, tuletist nimetaja nullidel ei eksisteeri)

4. Järjesta D( f) ja need punktid koordinaatjoonel.

5. Määrake tuletise märgid igal intervallil

6. Rakenda märke. 7. Kirjuta vastus üles.

3 min

V. Tunni kokkuvõte.õpilaste enesehinnang oma õppetegevuse tulemuste kohta.Viib läbi refleksiooni.

Mida uut sa tunnis õppisid?

Olid teie jaoks olemas huvitavaid hetki?

Kirjutage oma arvamus tunni kohta kleebistele.

Kaardid

2 minutit

VI.Kodutöö. Selgitab funktsioone kodutöö № 259, № 257

päevikutesse kirjutama.

Päevik

Kasvava funktsiooni definitsioon.

Funktsioon y=f(x) suureneb intervalliga X, kui mõne ja ebavõrdsus on rahuldatud. Teisisõnu, argumendi suurem väärtus vastab funktsiooni suuremale väärtusele.

Funktsiooni määratluse vähendamine.

Funktsioon y=f(x) väheneb intervalli jooksul X, kui mõne ja ebavõrdsus . Teisisõnu, argumendi suurem väärtus vastab funktsiooni väiksemale väärtusele.

MÄRKUS: kui funktsioon on defineeritud ja on pidev suurenemise või vähendamise intervalli lõpus (a;b), ehk millal x=a ja x=b, siis kaasatakse need punktid suurenemise või vähenemise intervalli. See ei ole vastuolus intervalli suureneva ja kahaneva funktsiooni definitsioonidega X.

Näiteks põhiliste elementaarfunktsioonide omaduste põhjal teame seda y = sinx on defineeritud ja pidev kõigi argumendi tegelike väärtuste jaoks. Seetõttu saame intervalli siinusfunktsiooni suurenemise põhjal väita intervalli suurenemist.

Äärmuspunktid, äärmusfunktsioon.

Punkti nimetatakse maksimaalne punkt funktsioonid y=f(x) kui kõigi jaoks x selle naabruses on ebavõrdsus tõsi. Kutsutakse funktsiooni väärtust maksimumpunktis funktsiooni maksimum ja tähistada .

Punkti nimetatakse miinimumpunkt funktsioonid y=f(x) kui kõigi jaoks x selle naabruses on ebavõrdsus tõsi. Kutsutakse funktsiooni väärtust miinimumpunktis funktsiooni miinimum ja tähistada .

Punkti naabrusena mõistetakse intervalli , kus on piisavalt väike positiivne arv.

Nimetatakse miinimum- ja maksimumpunktid äärmuslikud punktid, ja kutsutakse äärmuspunktidele vastavad funktsiooni väärtused funktsiooni äärmus.

Ärge ajage funktsiooni äärmusi segamini funktsiooni maksimaalse ja minimaalse väärtusega.

Esimesel joonisel funktsiooni suurim väärtus segmendil saavutatakse maksimumpunktis ja on võrdne funktsiooni maksimumiga ning teisel joonisel saavutatakse funktsiooni maksimaalne väärtus punktis x=b, mis ei ole maksimumpunkt.

Piisavad tingimused funktsioonide suurendamiseks ja vähendamiseks.

Funktsiooni suurenemise ja vähenemise piisavate tingimuste (märkide) alusel leitakse funktsiooni suurenemise ja vähenemise intervallid.

Siin on intervalli suurenemise ja kahanemise märkide sõnastused:

kui funktsiooni tuletis y=f(x) positiivne iga jaoks x intervallist X, siis funktsioon suureneb võrra X;

kui funktsiooni tuletis y=f(x) negatiivne mis tahes x intervallist X, siis funktsioon väheneb võrra X.

Seega on funktsiooni suurendamise ja vähenemise intervallide määramiseks vaja:

Vaatleme algoritmi selgitamiseks näidet suurenevate ja kahanevate funktsioonide intervallide leidmisest.

Näide.

Leia funktsiooni suurenemise ja kahanemise intervallid.

Otsus.

Esimene samm on funktsiooni määratluse ulatuse leidmine. Meie näites ei tohiks nimetaja avaldis seetõttu kaduda.

Liigume edasi funktsiooni tuletise leidmise juurde:

Funktsiooni suurenemise ja kahanemise intervallide määramiseks piisava kriteeriumi alusel lahendame võrratused ja definitsioonipiirkonnas. Kasutame intervallmeetodi üldistust. Lugeja ainus tõeline juur on x=2, ja nimetaja kaob kell x=0. Need punktid jagavad definitsioonipiirkonna intervallideks, milles funktsiooni tuletis säilitab oma märgi. Märgime need punktid numbrireale. Plusside ja miinustega tähistame tinglikult intervalle, millel tuletis on positiivne või negatiivne. Allolevad nooled näitavad skemaatiliselt funktsiooni suurenemist või vähenemist vastaval intervallil.